
Everyone (hopefully) knows there are many measures of risk in financial markets. The most commonly used example is volatility, but if your returns are skewed, you might want to focus only on the lower tail of the distribution, and if your losses are fat-tailed, you might want to use something like the Conditional Tail Expectation. But no matter what measure you use, you can't really measure risk.
Before I say why, let me contrast risk with something you sometimes can sort of measure: return. Actually, measuring return is very hard, because to measure the overall return of your portfolio, you have to measure the value of your assets. And that's hard. Just think of American banks, when they tried to value their mortgage-backed assets in the middle of the financial crisis. It was nearly impossible to mark assets to market, because there was no market - no one was buying. But "mark to model", i.e. using some theory to value the assets, was no better; it was rightly denigrated as "mark to myth".
As if that weren't enough, there's also the matter of price impact or slippage. When you try to sell stuff, the price will tend to change. That's a transaction cost, and it's an unpredictable transaction cost. So if I have a hundred tons of gold, it's hard to know how much I could get for that gold if I sold it all, even if I know the current price.
But if you liquidate all your investments, you can get cash, and since cash is the unit in which we denominate value (no "money is a bubble" stuff, please!), you can know your nominal return in that case...unless you count non-salable assets like human capital in your "portfolio", of course. And your real return, which depends on future inflation, is never quite calculable.
But compared to risk, return is peanuts to measure. Why? Because risk is all about counterfactuals.
Return can't be known in advance, obviously, but if you can mark to market and if you ignore price impact, you can measure your return after the fact. Not so with risk. Risk not only can't be known in advance, it can't be known in retrospect either. Suppose I buy GM stock, hold it for a year, and then sell. How much risk did I incur over that period? First of all...who cares? It's over and done. But even if I did care, I couldn't know, because what actually happened to my asset reveals little about what might have happened.
For example, the realized volatility of the asset over that holding period tells me little. First of all, it didn't end up mattering for my eventual return. Second of all, I might have been able to time the ups and downs, buying when it was cheap or selling when expensive. And knowing how likely I would have been to successfully time the returns is incredibly difficult.
But also, the realized volatility doesn't tell us how likely volatility was to change over that period. See, volatility changes. Over at his blog Keplerian Finance, Stony Brook applied math prof and long-time hedge-fund maestro Robert Frey does a quick calculation of S&P volatility, and identifies what look like distinct regimes. He bins them up into the following picture:
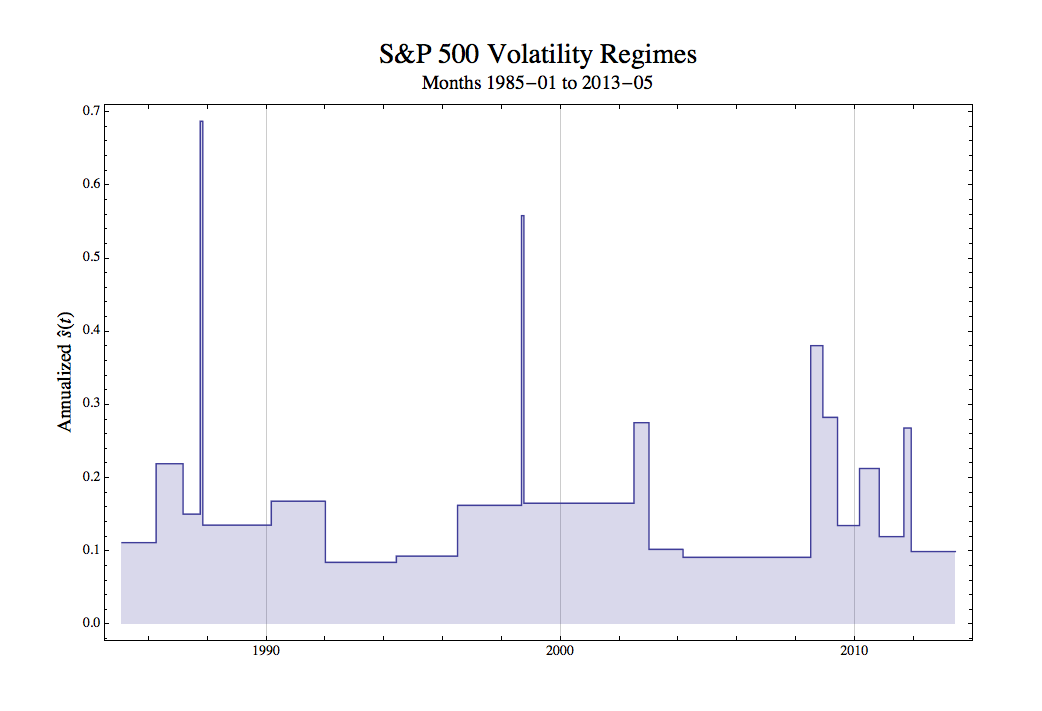
As you can see, volatility is mostly constant, but has a few extremely spiky spikes. Whatever is causing those spikes, they're too rare and too irregular to get a good idea of how likely you are to hit a spike in any given year.
So suppose your GM stock didn't have a ton of volatility over the year in which you held it. No spikes. But what were the chances of one of those spikes happening over that year? You don't really know. So that means you don't really know if whatever return you ended up making was justified by the risk.
You'll never know how closely you dodged a bullet.
One interpretation of this is that there's always true Knightian uncertainty in the world. Another is that there's only risk (i.e. probabilities are fixed), but we'll always have great difficulty estimating it from data. The difference is mostly philosophical; effectively, those are the same thing. Andrew Lo goes into a lot more depth on the topic in this famous paper.
Now this doesn't mean we can know nothing about risk. Obviously we can know something about it - measures like volatility or conditional tail expectation are useful. But not only will we never know everything about risk, we'll never know how much we know about it; at any time, our quantitative measures of risk might be getting more informative or less informative, as Frey's graph shows pretty clearly.
So how should we react to the unknowability of risk? Should we simply assume that the "true" distribution is so fat-tailed that we should avoid taking chances as much as possible? Probably not, since over many stretches of time, people who assume that "true" risk is small (distributions are thin-tailed) will sometimes end up being correct for a very long time. And for that very long time, the risk-ignorers will prosper much more than the risk-suspecters.
In fact, there is no optimal solution. Sometimes we'll guess there's more risk than there actually is, and sometimes we'll guess less. And we'll never know which of our guesses were right, or whether we just dodged a bullet we never saw.
Tidak ada komentar:
Posting Komentar